Designed or Designoid
Richard Dawkins begins climbing Mount Improbable by contrasting two rock formations (Dawkins, 1996). The first is a weathered hillside in Hawaii that, when it is viewed from a certain direction at a certain time of day at a certain time of the year, casts a shadow that has a resemblance to John F. Kennedy. The second is the magnificent Mount Rushmore in South Dakota, where the images of Presidents Washington, Jefferson, Theodore Roosevelt and Lincoln are clearly seen from any angle at any time of the day, any season of the year. Obviously the weathered hillside in Hawaii is the result of pure accident while the faces on Mount Rushmore were carefully designed. Dawkins goes on to claim that living systems in nature look as though they, like Mount Rushmore, were designed but can be explained naturalistically. Dawkins calls such objects in nature “designoids.” The character of the cosmos, particularly the coincidence that the universal constants are indeed what they need to be to provide a suitable home for life, must also be a designoid in Dawkins’s thinking. In fact Dawkins’s materialistic philosophy would lead him to assign the label designoid to all facets of nature that give the appearance of design, assuming as he does the nonexistence of a creator or a designer (see Dawkins, 1986). The purpose of this chapter is to show that not every facet of nature that appears designed is merely a designoid, but rather that nature includes facets that may rightly be regarded as designed.
Possible Designoids
We therefore consider three possible designoids:
- The physical universe is surprising in the simple mathematical form it assumes. All the basic laws of physics and fundamental relationships can be described on one side of one sheet of paper because they are so few in number and so simple in form (see table 1.1).
- The universal constants that are needed in these mathematical descriptions of the laws of nature (table 1.1) and the fundamental properties of matter in nature (such as unit charge, mass of electron, mass of proton, etc.) must be carefully prescribed if a universe suitable not just for life as we know it but suitable for life of any imaginable type is to be possible. The values of some of these constants are provided in table 1.2.
- The existence of living systems requires the specification of some very complex boundary conditions, such as the sequencing required to get functional biopolymers. As Michael Polanyi noted some years ago, both machines and living systems transcend simple explanations based on the laws of chemistry and physics, requiring as they do highly improbable initial conditions or time independent boundary constraints (Polanyi 1967).
Polanyi illustrated his argument with a discussion of an automobile. The operation of every part of the automobile can be fully explained in terms of principles of chemistry and physics. When the piston is lowered, air and vaporized gasoline are drawn into the cylinder. This mixture is subsequently compressed as the piston rises to the top of its stroke. A spark ignites the mixture, allowing the reaction of the oxygen in the air with the gasoline, releasing a large amount of energy. This released energy causes tremendous pressure on the piston, which is then displaced downward. This downward motion is transmitted to the drive shaft as torque, which is then transmitted to the wheels of the car, completing the transformation of chemical energy in the gasoline into kinetic energy of the moving automobile. Every step can be nicely explained by the laws of chemistry and physics. Yet these laws cannot account for the existence (i.e., origin) of the automobile, but only for its operation. The highly unusual (boundary) conditions under which the chemical energy in the gasoline is converted into kinetic energy in the automobile are the result of careful design of the system and its component parts by a mechanical engineer who subsequently passed the drawings to a skilled machinist who fabricated the pieces and then gave them to a mechanic who assembled the pieces in just the right fashion. Human intelligence is a crucial factor in the existence of a functional automobile. Polanyi argues that living systems are far more complicated than the machines of people and thus provide an even greater challenge to the observer to explain their exist ence in terms of natural laws alone.
|
Table 1.1: Fundamental Laws of Nature |
Mechanics (Hamilton’s Equations)
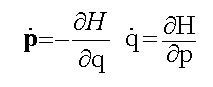
Electrodynamics (Maxwell’s Equations)
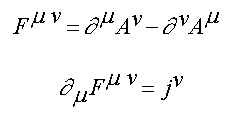
Statistical Mechanics (Boltzmann’s Equations)
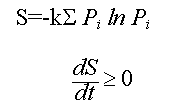
Quantum Mechanics (Schrödinger’s Equations)
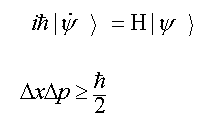
General Relativity (Einstein’s Equation)
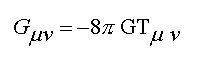
| Universal Constants |
| Mass of Elementary Particles |
| Fine Structure of Constants |

Critical Issues in Designed or Designoid Systems
At the human level the engineer can deal only with prescribing boundary conditions, having no control over the laws of nature, the universal constants or the fundamental properties of matter. It is important to emphasize that in the prescribing of boundary conditions, the challenge is not to establish order but rather complexity. Much of the discussion in the scientific literature does not make this distinction and thus wrongly argues that self-ordering can somehow solve the boundary condition problem. The regular arrangement of atoms in a crystal bear scant resemblance to the informational requirements of a biopolymer. Thaxton, Bradley and Olsen (1984) emphasized that the informational requirements needed to construct a crystal are quite small. Specify the requirements for the unit cell (the smallest subdivision of the crystal that retains all of the essential symmetry features) and then just repeat infinitum. However, to make a functional protein for a DNA molecule, one must specify the sequencing for a very large number of amino acid units in protein or bases in DNA. Function in biopolymers is inextricably connected to the specific aperiodic sequence of building blocks, and it is this specification of sequence to which I refer as biological information. This distinction is developed in detail by Steven C. Meyer in chapter five of this volume.
In an analogous way the same type of problem attends cosmology. A universe that is suitable to support life seems to require a very narrow prescription of the various universal constants. Whether biological and cosmological information can be accounted for in some naturalistic way, as claimed by Dawkins (1986, 1996), or is the result of activity by an intelligent designer who works on a cosmic scale, much like the mechanical engineer who designs a car, is the crucial issue to be addressed in this chapter and by the other chapters in this volume.
Proposed Designoid Solutions to the Appearance of Cosmological and Biological Design
The most prominent and promising proposed solution to the apparent design in cosmology are string theory and the unified field theory (Weinberg 1992). It is claimed that these theories may eventually explain why many of the universal constants have exactly the values that they must (cosmological information for our design or designoid universe) to provide a universe that is suitable not just for life as we know it but for life of any imaginable type.
During the last fifty years, however, at least seven natural explanations for biological design have been proposed to account for biological information: time plus chance; natural ordering due to equilibrium thermodynamics; irreversible (nonequilibrium) thermodynamics; intrinsic chemical bonding preferences; self-organizing systems; complexity from simple algorithms; and mutation or natural selection.
The three most prominent currently are Dawkins’s incrementalist approach via mutation or natural selection (Dawkins 1986, 1996), Prigogine’s irreversible thermodynamics of nonlinear systems (Prigogine 1980) and Kauffman’s self-ordering systems (Kauffman 1993, 1995). Each claims to provide immediately or have the potential to provide eventually a naturalistic explanation that is adequate to account for biological information, making all biological appearances of design in actuality designoids. In what follows, each of these proposals will be critiqued to see to what degree they can immediately or may ultimately provide a sufficient cause to account for the informational results we see in the cosmos and in living systems, rendering the universe a designoid rather than a true design by an intelligent creator or designer.
Design or Designoid: The Mathematical Form That Nature Takes
It has been widely recognized for some time that nature assumes a form that is elegantly described by a relatively small number of simple, mathematical relationships, as previously noted in table 1.1. None of the various proposals presented later in this chapter to explain the complexity of the universe address this issue. Albert Einstein in a letter to a friend expressed his amazement that the universe takes such a form (Einstein 1956), saying:
You find it strange that I consider the comprehensibility of the world to the degree that we may speak of such comprehensibility as a miracle or an eternal mystery. Well, a priori one should expect a chaotic world which cannot be in any way grasped through thought. . . . The kind of order created, for example, by Newton’s theory of gravity is of quite a different kind. Even if the axioms of the theory are posited by a human being, the success of such an enterprise presupposes an order in the objective world of a high degree which one has no a priori right to expect. That is the “miracle” which grows increasingly persuasive with the increasing development of knowledge.
Alexander Polykov (1986), one of the top physicists in Russia, commenting on the mathematical character of the universe, said: “We know that nature is described by the best of all possible mathematics because God created it.” Paul Davies, an astrophysicist from England, says, “The equations of physics have in them incredible simplicity, elegance and beauty. That in itself is sufficient to prove to me that there must be a God who is responsible for these laws and responsible for the universe” (Davies 1984). Successful development of a unified field theory in the future would only add to this remarkable situation, further reducing the number of equations required to describe nature, indicating even further unity and integration in the natural phenomena than have been observed to date.
Design or Designoid:
Setting the Values of the Universal Constants — Prescribing the Cosmological Information
The remarkable coincidences that the universal constants (see table 1.2) are just what they need to be to provide a universe suitable for life of any imaginable type have been well documented in a series of books published in the past ten years (e.g., Davies 1988; Tipler and Barrow 1986; Breuer 1991; Gribbins and Rees 1993). It is useful to highlight a few of these coincidences to illustrate the physical nature of cosmic informational requirements to provide a suitable home for life of any imaginable type. While life does not necessarily have to assume the form that it has on earth (or in our universe), it is possible to identify minimal requirements that would apply for life of any imaginable type. These would include such requirements as a reasonable amount of elemental diversity to provide for the molecular complexity to process energy, store information and replicate (which are minimal functions for living systems) and a reasonably stable source of energy such as is provided by our sun.
Brandon Carter in 1970 showed that a 2 percent reduction in the strong force and its associated constant would preclude the formation of nuclei with larger numbers of protons, making the formation of elements heavier than hydrogen impossible. On the other hand, if the strong force and associated constant were just 2 percent greater than it is, then all hydrogen would be converted to helium and heavier elements from the beginning, leaving the universe no water and no long-term fuel for the stars. The absolute value of the strong force constant, and more importantly, its value relative to the electromagnetic force constant is not “prescribed” by any physical theories, but it is certainly a critical requirement for a universe suitable for life (Breuer 1991, 183). Carter has also shown that the existence of a sun such as our own that provides the long-term source of energy required for the existence of life depends on the very precise specification of the gravity force constant, the electromagnetic force constant, the mass of the proton and the mass of the electron. It is remarkable that the values of these four apparently independent physical constants are exactly what they must be to provide for a long-term source of energy such as our sun provides.
The existence of elements heavier than beryllium is again the result of the remarkable coincidence first predicted by Hoyle (Hoyle et al. 1953) and later confirmed experimentally of a quantum energy level in carbon at exactly the value needed to provide for a very efficient conversion in a fusion reaction from beryllium (reacting with helium) to carbon and a partially efficient conversion of carbon (reacting with helium) to oxygen, leaving an ample supply of both. The existence of this precise energy level in carbon in turn is the consequence of the very precise values of the strong force and the electromagnetic force constants.
More than one hundred similar cosmological coincidences have been identified. Initially there was a tendency to attribute these coincidences to fortuitous accidents, as evidenced by an early quotation from Hoyle (1951, 103-4):
I have often seen it stated that our situation on earth is providential. The argument goes like this. It is providential that the earth is of the right size and at the right distance from the sun. It is providential that the sun radiates the right kind of heat and light. It is providential that the right chemical substances occur on earth. A long list of this sort of statements could be compiled, and to some people it looks as if there is indeed something very strange and odd about our particular home in the universe. But I think that this outlook arises from a misunderstanding of the situation. Because if everything was not just right we should not be here. We should be somewhere else (or more likely, no where).
However, many scientists are no longer willing to attribute these coincidences to chance, as is evidenced by a much more recent quotation from Hoyle: “Such properties seem to run through the fabric of the natural world like a thread of happy coincidences. But there are so many odd coincidences essential to life that some explanation seems required to account for them” (Hoyle 1983, 220). Arno Penzias, Nobel laureate in physics and the director of Bell Laboratories until its recent fragmentation, makes this observation about the enigmatic character of the universe: “Astronomy leads us to a unique event, a universe which was created out of nothing, and delicately balanced to provide exactly the conditions required to support life. In the absence of an absurdly-improbable accident, the observations of modern science seem to suggest an underlying, one might say, supernatural plan” (Brock 1992).
In summary it is clear that providing a universe that is suitable for life requires a remarkable assignment of the values for the various universal constants. The source of this cosmological information requires some explanation. How may these remarkable coincidences be explained in terms of natural laws? At present none of the explanations to be discussed with regard to biological information and design have any bearing on cosmological information and design. It has been suggested that a unified field theory might show that certain of the constants are causally connected to each other so that they are not independently assigned. However, in such a theory the residual constants would almost certainly need to be prescribed even more narrowly. Why these constants happen to be exactly what they need to be when they could in principle assume any value does not seem to be reducible to a naturalistic cause or explanation.
Design or Designoid: The Origin of Biological Information
We now consider the seven possible natural explanations for how biological information might be created.
Random chance. It was fashionable in the middle part of the twentieth century to attribute biological information and complexity to chance plus time (Monod 1972). However, as our understanding of the enormous biochemical complexity associated with the origin of life and the development of more complex life forms has matured, appeals to chance have gradually lost credibility. Appeals to chance have been further hurt by the recognition that the universe is not infinitely old. In fact the widespread acceptance of the big bang cosmology after the discovery of background radiation in 1965 caused chance to lose favor very quickly as a suitable explanation for the origin of life (Kenyon and Steinman 1969). It would be fair to say that chance is nothing more than the God of the gaps of the atheist, expressing as an article of faith what reason cannot demonstrate.
Spontaneous ordering near equilibrium — phase changes.
It is common for proponents of naturalistic sources of biological information resulting in designoids to use analogies to simple phase changes in nature in which disordered systems become spontaneously ordered, as when randomly arranged water molecules become highly ordered molecules in an ice crystal or a snowflake. However, this solution can be easily understood to be the simple result of providing a chemical energy driving force that is sufficiently strong to overcome the natural tendency to disorder when the temperature is reduced to a sufficiently low value (below the melting point). The melting point in fact is thermodynamically determined by the ratio of the change in enthalpy (mainly chemical bonding energy) during the phase change divided by the associated change in the entropy of the system. Details of this argument have been presented elsewhere (Thaxton, Bradley, and Olsen 1984; Meyer, chap. 5 in this volume).
An analogy may be helpful. If I have a pool table with a dip in the center of the table and I gently agitate the table, I would expect in due course to find all of the balls in the dip in the center of the table, since this represents the position of lowest potential energy. However, this explanation is irrelevant to the formation of biopolymers and biological information for two reasons. First, the change in the enthalpy in the polymerization of biopolymers is positive (needs energy to be supplied, endothermic) rather than negative (gives off energy, exothermic), which would correspond to a hump in the center of the pool table. This makes the polymerization process much more difficult. Second and more importantly, the order in crystals has very little information and thus does a poor job of mimicking the specified aperiodicity in the sequencing of functional biopolymers, which is very information-intensive.
It is worth noting that all living systems live energetically well above equilibrium and require a continuous flow of energy to stay there (much as a hot water heater maintains hot water above the equilibrium temperature of the room). Equilibrium is associated with death in the biosphere, making any explanation of the origin of life that is based on equilibrium thermodynamics clearly incorrect. In summary phase changes such as water freezing into ice cubes or snowflakes is irrelevant to the processes necessary to generate biological information.
Prigogine’s spontaneous self-organization in irreversible thermodynamic systems far from equilibrium.
Prigogine’s work is based on much more significant analysis and supporting experiments than is Dawkins’s while making much more modest claims of progress. The self-organization Prigogine (Prigogine 1980; Prigogine, Nicolis, and Babloyantz 1972) can predict and demonstrate experimentally requires the following conditions: the system must be open and subject to a constant input and output of matter and energy, implying systems constrained to be far from equilibrium; various catalytic, cross-catalytic or feedback processes must be present in the system, insuring that the description of the system kinetics will include nonlinear differential equations; and certain well-defined values of imposed constraints must be imposed so that fluctuations are not damped but can grow.
The nature of the self-organization that is predicted and empirically demonstrated by Prigogine and others in this field of irreversible thermodynamics is spontaneous spatial ordering and/or time-dependent cycling in a system. While such behaviors constitute an increase in the complexity of the behavior of the system compared with that observed at equilibrium, it is more the type of order that we see in crystals, with little resemblance to the type of complexity that is seen in biopolymers.
Autocatalytic activity in RNA could provide the possibility of similar behavior in a biological system, if the system has the necessary constraints and system parameters specified. However, the nature of the outcome would be more polymerization of RNA-like chain segments but with no assistance in sequencing. Again, this whole approach does not seem capable of generating the aperiodic, specified complexity that is usually associated with biological information essential to life.
In an article dealing with self-organization in irreversible thermodynamic systems, Prigogine, Nicolis and Babloyantz (1972) indicated that they were “tempted to hope” that such phenomena might one day explain how one gets from molecules to man. Fourteen years later, in the most recent book highlighting their work in this area, Babloyantz (1986, 220) comments wistfully,
The bold and audacious hypothesis which assumes that life has been created as a result of the self-organization of matter is new. At the present time it seems the only valid hypothesis which reconciles matter and life. Ultimately, such an idea must be confirmed in laboratory experiments. We are at the very beginning of such an endeavor, and the road from molecules to life is still very long and full of pitfalls. However, we are entitled to HOPE that sometime in the future it can be proved unambiguously that self-organized properties of reacting and flowing systems constitute the missing link in the evolution of molecules to man.
Prigogine’s group has made remarkable progress in showing how highly constrained systems meeting certain parametric requirements can self-organize. However, this self-organization does not yet seem to provide any useful path to biological information.
Physical or chemical forces in nature.
Steinman and Cole (1967) published a paper in the National Academy of Science’s Proceedings that purported to demonstrate that sequencing of amino acids in proteins is not random (or by chance, which proved to be too improbable) but rather depends on the variations in the affinity of various amino acids for one another. Support for this hypothesis was presented which was based on the number of dipeptide bonds formed in a solution in which amino acids were allowed to react to form dipeptides. The observed dipeptide bond frequencies were then compared with the sequencing of amino acids for ten actual proteins and were found to correlate nicely. Thus for a time it was thought that this chemical affinity might be able to account for the amino acid sequencing in proteins.
Subsequent work by Kok, Taylor, and Bradley (1988), however, has clearly demonstrated that the original amino acid dipeptide bond frequencies for the ten actual proteins reported by Steinman and Cole were incorrect. Furthermore, when dipeptide bonds frequencies from 250 different proteins taken from the Atlas of Protein Sequence and Structure (Dayhoff 1965) were considered, the frequency was found to correlate much better with random statistical probabilities than with the experimentally measured dipeptide bond frequencies of Steinman and Cole.
There is a more fundamental reason for doubting that chemical affinities can account for biological information. If the steric interference between various proteins was strong enough to determine sequencing, then one would expect to get only one or possibly a few sequences. The great variety of sequences noted in different proteins argues strongly for an explanation other than intrinsic physical or chemical forces in nature. Furthermore, sequencing of bases in DNA could not have been explained in this way in any case since the backbone chain bonds are all identical, with the bases as side chains off the backbone.
Kauffman and Santa Fe Institute’s approach to complexity and self-organization.
As it has become more widely recognized that the complexity of even the simplest imaginable living thing defies piecewise assembly in a prebiotic soup or elsewhere, scientists have looked for promising alternative paradigms to the traditional “soup theory” to explain both the origin and development of the complexity that is ubiquitous in nature. Stuart Kauffman (1993, 1995) of the Santa Fe Institute is the leading proponent of the most popular new paradigm. Accordingly complexity results naturally from the self-organizing character of nature. In two recent books Kauffman (1993, technical; 1995, shorter and less technical presentation of the same ideas) argues that the origin of “life” is essentially inevitable, not vastly improbable as Jacques Monod (1972), Francis Crick (1981), Robert Shapiro (1986) and the present author have previously argued (Thaxton, Bradley, and Olsen 1984).
Kauffman defines “life” as a closed network of catalyzed chemical reactions that reproduce each molecule in the network—a self-maintaining and self-reproducing metabolism that does not require self-replicating molecules. Kauffman’s ideas are based on computer simulations alone without any experimental support. He argues with his computer simulations that when a system of simple chemicals reaches a critical level of diversity and connectedness, it undergoes a dramatic transition, or phase change. Kauffman further postulates that molecules in such a system undergo a dramatic transition, combining to create larger molecules of increasing complexity and catalytic capability—Kauffman’s definition of life.
Such computer models ignore important aspects of physical reality that, if they were included in the models, would make the models not only more complicated but also incapable of the self-organizing behavior that is desired by the modelers. For example, Kauffman’s origin of life model requires a critical diversity of molecules so that there is a high probability that the production of each molecule is catalyzed by another molecule. For example, he posits 1/1,000,000 as the probability a given molecule catalyzes the production of another molecule (which is too optimistic a probability based on catalyst chemistry). If one has a system of 1,000,000 molecules, then in theory it becomes highly probable that most molecules are catalyzed in their production, at which point this catalytic closure causes the system to “catch fire,” effectively to come to life (Kauffman 1995, 64).
Einstein said that we want our models to be as simple as possible but not too simple (i.e., ignoring important aspects of physical reality). Kauffman’s model for the origin of life ignores critical thermodynamic and kinetic issues that, if they were included in his model, would “kill” his “living system.” For example, there are kinetic transport issues in taking Kauffman’s system with 1,000,000 different types of molecules, each of which can be catalyzed in its production by approximately 1 type of molecule, and organizing it in such a way that the catalyst that produces a given molecule will be in the right proximity to the necessary reactants to be able to be effective. Kauffman’s simple computer model ignores this enormous organizational problem that must precede the “spontaneous self-organization” of the system. Here he is assuming away (not solving) a system-level configurational entropy problem that is completely analogous to the molecular-level configurational entropy problem discussed in Thaxton, Bradley, and Olsen (1984).
Kauffman does acknowledge that polymerization of biopolymers goes uphill energetically, an important physical reality that is also ignored in his simple model. His three proposed solutions to this problem all complicate his simple model in ways that are untenable. For example, he suggests that coupling the energetically unfavorable polymerization reactions with other energetically favorable chemical reactions could solve the thermodynamic problem, but he fails to recognize that this dramatically increases the logistical problems in kinetic transport mentioned previously, solving the chemical energy (enthalpy) problem while enlarging the configurational entropy problem. Dehydration and condensation onto substrates, his other two possible solutions to the thermodynamic problems, also further complicate the logistics of allowing all of these 1,000,000 molecules to be organized into a system in which all catalysts are rightly positioned relative to reactants to provide their catalytic function, again significantly increasing the configurational entropy problem.
It would be useful to quantify the magnitude of increase in the configurational entropy barrier that is implicit in each of Kauffman’s solutions to the physical shortcomings he acknowledges in his model, as well as the shortcomings he apparently does not recognize or at least acknowledge as Thaxton, Bradley, and Olsen (1984) have previously done for biopolymers. Unfortunately he does not provide sufficient details in his model to allow such a calculation to be made, and any calculation would be very model-specific. However, given the number of items to be arranged and the specificity needed to give function, it would most likely be much greater than that associated with a biopolymer.
Kauffman’s (1995, chap. 3) origin-of-life discussion is entitled “A Chemical Creation Myth,” which it truly is. Chapter four is entitled “Order for Free.” But Kauffman’s “self-ordering” only appears to be free because he ignores the thermodynamic and kinetic realities, which incur the “real costs of this ordering.”
John Horgan (1995) quotes W. Brian Arthur of the Santa Fe Institute as saying, “If Darwin had a computer on his desk, who knows what he could have discovered.” Horgan then wryly comments, “What indeed: Charles Darwin might have discovered a great deal about computers and very little about nature.” Horgan describes the entire field of complexity as being based on a seductive syllogism: There are simple sets of mathematical rules that when followed by a computer give rise to extremely complicated patterns. The world contains many extremely complicated patterns. Conclusion: Simple rules underlie many extremely complicated phenomena in the world. Horgan quotes John Maynard-Smith, one of the pioneers of mathematical biology, as referring to such simulation science as “fact-free science,” where mentioning observational facts is considered to be in bad taste. Horgan concludes that given our lack of knowledge of how life might arise here or elsewhere, whether life began as Kauffman and his colleagues at the Santa Fe Institute say is entirely a matter of speculation, and all the computer simulations in the world cannot make it less so.
Simple algorithms as a source of information.
In those portions of Kauffman’s (1993, 1995) books that deal with evolution rather than the origin of life, he employs computer simulations of Boolean networks to show that simple algorithms can produce complex patterns. In a vague analogy to biology, he infers that nature can likewise produce biological complexity. However, one must not forget that the simple algorithms on which Kauffman bases the analogy operate on a very complex computer to produce the observed cyberspace complexity. The problem in nature is that one must find not only appropriately simple algorithms but also the computer in which the simple algorithm can operate to generate complexity. You do not get something (i.e., complexity) for nothing (i.e., a simple algorithm).
Dawkins (1986) also resorts to computer algorithms to support his argument that biological information can be generated easily via natural selection with a computer simulation entitled The Blind Watchmaker. What he demonstrates is that a very sophisticated computer system with a relatively simply algorithm can produce a variety of patterns on the computer screen, some surprisingly complex. This analogy fails to explain the origin of complexity in nature for two reasons. First, he begins with a very sophisticated computer bootlegging in a high degree of complexity to his starting point. Second, he has failed in the ten years since he first published The Blind Watchmaker book and computer simulation to point out any processes in nature that would be examples of his computer algorithms. If this is indeed how complexity is generated in nature, why are examples so hard to find?
In 1986 Dawkins offered one thousand dollars to the first person who could create an algorithm that could produce a certain biomorph. Both the first- and second-place finishers in this contest indicated that an algorithm alone could not produce the required biomorph (Pittman 1989). Without building “design” into the system to give some direction and constraint, the biomorph could not be produced, which is probably analogous to the real situation in nature.
Dawkins’s incremental approach to information generation.
Dawkins in his most recent books (1986, 1996) argues strongly that random mutations in combination with highly directed natural selection can account for all biological information. He presses his argument not with empirical data but with cleverly devised analogies from nature and from computer-generated biomorphs. What is the substance of these arguments?
In Climbing Mount Improbable, Dawkins cheerfully admits that living systems cannot possibly be created in one improbable step any more than Mount Improbable can be scaled on its nearly vertical face in one gigantic and improbable step. However, he argues that by coming up the back side in many small steps, it can be scaled. He acknowledges the difficulty in larger steps that require macromutations, expressing some differences with Gould about just how large of a mutation is likely to occur. For this analogy to be meaningful, however, Dawkins’s tacit assumption is that there is a way to the top of the mountain that can be climbed like a well-honed footpath, a path carefully put into place by the park rangers so climbers can avoid any larger steps.
Mutations produce the change in information while natural selection is the source of improvement in the quality of the information. However, this process cannot take the larger steps that are associated with the origin of light-sensitive cells in an organism, for example. Thus Dawkins’s journey to the top of Mount Improbable is possible only if the path can realistically be made in a large number of small steps. Michael Behe (1996) clearly demonstrates this is not the case, rendering Dawkins’s argument untenable.
Dawkins’s bold claims to tell us how Mount Improbable may be scaled offers no fundamental principles of promise regarding how biological information of the scale needed to explain macroevolution might be generated and absolutely no empirical support for his thesis that there is a footpath to the top of Mount Improbable with sufficiently small steps. In a recent letter to the editor of The Independent Brian Josephson, professor of physics at Cambridge University, summarizes Dawkins’s approach:
In such books as the Blind Watchmaker, a crucial part of the argument concerns whether there exists a continuous path, leading from the origins of life to man, each step of which is both favored by natural selection, and small enough to have happened by chance. It appears to be presented as a matter of logical necessity that such a path exists, but actually there is no such logical necessity; rather, commonly made assumptions in evolution require the existence of such a path. (Josephson, 1997)
Conclusion
Not only has science failed to provide naturalistic explanations for the mathematical form of nature, the coincidence of cosmological constants, and the emergence of living things, but also these facets of nature all demonstrate the essential element of design, namely, information. Various naturalistic explanations for this biological and cosmological information have been reviewed and found wanting.
Chance and intrinsic chemical properties of matter have both been considered and abandoned as unreasonable explanations for the complexity we see in the character of the universe and in biological systems. The ordering that results from a local decrease in enthalpy (as in a phase change) cannot account for cosmological or biological information but only for the kind of ordering that is seen in crystals.
Constraint of systems far from equilibrium can produce self-organization that takes the form of spatial ordering and/or cycling over time. However, neither biological information (e.g., aperiodic specificity in sequencing of biopolymers) nor cosmological information is created in such processes. The limited ordering and information produced in such systems is consistent with the information level of the constraints imposed on the system.
Self-organization in complex systems that consists of large numbers of chemicals coupled together have been demonstrated primarily in computer simulations. Again the complexity or information that can be produced in an actual system depends on logistically arranging the many chemical reactions that take place in a very complicated way so that the required coupling can occur. While this is not a problem in the computer, it would be a nightmare in a real system of 1,000,000 chemical reactions. In reality the information associated with the self-organization in such systems is almost certainly less than the informational requirements to make the necessary spatial arrangements. Again we see that there do not seem to be any free lunches in nature when one is trying to explain the origin of information.
Natural selection acting on mutationally induced random change in the genetic code can produce biological information where the steps are small, what we normally associate with microevolution. The origin of new systems such as sight, which begins with irreducible complexity of a light-sensitive cell, cannot be accounted for by mutation or natural selection alone. Only the gently rolling high pastures on the back side of Mount Improbable can be crossed by this process, and you cannot reach the top of Mount Improbable by passing only through gently rolling high pastures. No cosmological information (i.e., finely tuned cosmological constants) results from mutation or natural selection.
The similarity between such information in nature and the production of information by human intelligence argues persuasively for an intelligent creator or designer. Consistent with this hypothesis is the utter failure of all natural processes that have been identified to date to account for biological and cosmological information. Our best scientific evidence supports a universe that is designed and not merely a designoid.
A reprint of Chapter 1 (pp. 33–50) from Mere Creation: Science, Faith and Intelligent Design, William A. Dembski, Ed. (Intervarsity Press, 1998). Used by permission.
References
- Babloyantz, A. 1986. Molecules, dynamics and life. New York: Wiley & Sons.
- Behe, M. 1996. Darwin’s black box. New York: Simon and Schuster.
- Breuer, R. 1991. The anthropic principle: Man as the focal point of nature. Boston: Birkhauser.
- Brock, D. L. 1992. Our universe: Accident or design? Wits, South Africa: Star Watch.
- Crick, F. 1981. Life itself. New York: Simon and Schuster.
- Davies, P. 1984. Superforce. New York: Simon and Schuster.
- ———. 1988. The cosmic blueprint. New York: Simon and Schuster.
- Dawkins, R. 1986. The blind watchmaker. New York: Norton.
- ———. 1996. Climbing Mount Improbable. New York: Norton.
- Dayhoff, M. O. 1965. Atlas of protein sequence and structure. Silver Springs, Md.: National Biomedical Research Foundation.
- Einstein, A. 1956. Lettres a Maurice Solovine. Paris: Gauthier-Villars.
- Gribbins, J., and M. Rees. 1989. Cosmological coincidences: Dark matter, mankind and anthropic cosmology. New York: Bantam.
- Horgan, J. 1995. From complexity to perplexity. Scientific American 272, no. 6 (June):104-9.
- Hoyle, F. 1951. The nature of the universe. New York: Harper.
- ———. 1983. The intelligent universe. London: Michael Joseph.
- Hoyle, F., D. N. F. Dunbar, W. A. Wensel, and W. Whaling. 1953. Physics Rev. 192:649.
- Josephson, B. 1997. Letter to the editor. The Independent, January 12.
- Kauffman, S. 1993. Origins of order: Self-organization and selection in evolution. New York: Oxford University Press.
- ———. 1995. At home in the universe: The search for laws of self-organization and complexity. New York: Oxford University Press.
- Kenyon, D. H., and G. Steinman. 1969. Biochemical predestination. New York: McGraw-Hill.
- Kok, R. A., J. A. Taylor, and W. L. Bradley. 1988. A statistical examination of self-ordering of amino acids in proteins. Origin of Life and Evolution Biosphere18:135-42.
- Monod, J. 1972. Chance and necessity. New York: Vintage.
- Pittman, T. 1989. Another look at the blind watchmaker. Origins Research (spring/summer):10-11.
- Polanyi, M. 1967. Life transcending chemistry and physics. Chemical and Engineering News, November, 45:54-64.
- Polykov, A. 1986. Scientists at the frontiers. Fortune, October 13, 47-57.
- Prigogine, I. 1980. From being to becoming. New York: Freeman.
- Prigogine, I., G. Nicolis, and A. Babloyantz. 1972. Physics Today, November, 23-31.
- Shapiro, R. 1986. Origins: A skeptic’s guide to the creation of life in the universe. New York: Simon and Schuster.
- Steinman, G., and M. Cole. 1967. Proceedings of National Academy of Science USA 58:735.
- Thaxton, C. B., W. L. Bradley, and R. L. Olsen. 1984. Mystery of life’s origin: Reassessing current theories. Dallas: Lewis and Stanley.
- Tipler, F. J., and J. D. Barrow. 1986. The anthropic cosmological principle. New York: Oxford University Press.
- Weinberg, S. 1992. Dreams of a final theory. New York: Pantheon.
